World Generation - The Beginning, and Now
As you may have noticed already, this game uses procedural generation to create an infinite world.
This includes multiple different biomes, each with their own combinations of colours and decorations, as well as which items or other points of interest can spawn there (and how rarely).
Of course, all of that didn't appear out of thin air, and I needed to start at the beginning.
The first step to world generation, in this case with hexagons, was figuring out the mathematical formula that would get those hexagons into the correct positions consistently.
For multiple reasons, I didn't really want to just copy and paste something from just any other game with a hexagonal grid (after all, there was no guarantee that other games would end up with the features I might end up needing). In addition, I felt up to the challenge of figuring it out bit by bit.
So my first attempt was to try to figure it out from first principles.
I knew how square grids worked, mathematically speaking.
They had two axes, an X axis and a Y axis (or an X and a Z, depending on how you look at it), and every square could be uniquely identified by it's position along those two axes.
For example, the square at position "5, 3" would be 5 positions along the X axis, and 3 positions along the Z axis. If the squares and grid used regular units, you could also measure in those distances.
Meaning, say, if there were some sort of game that was made of 1 metre cubes, then cube "5, 3" would be 5 position, 5 cubes, and 5 metres along the X axis.
This is pretty easy for squares, since you only need 2 axes, and they have only 4 sides (one for each direction along an axis).
Hexagons are a bit more difficult, since they have 6 sides, implying 3 axes.
(Plus, square grids are naturally aligned with 2 of the 3 axes of 3d coordinates in game engines. In hexagonal grids every other hex in an East-West line needs to be offset slightly to either the North or South).
That was, until I looked at it from the right angle and realised that it would be possible to fill a hexagonal grid using only 2 axes, but one of them would need to be a diagonal axis. This made it a lot easier to calculate the positions of all the hexes and (at first) only made it slightly more difficult to calculate the distance between certain hexes.
The result?
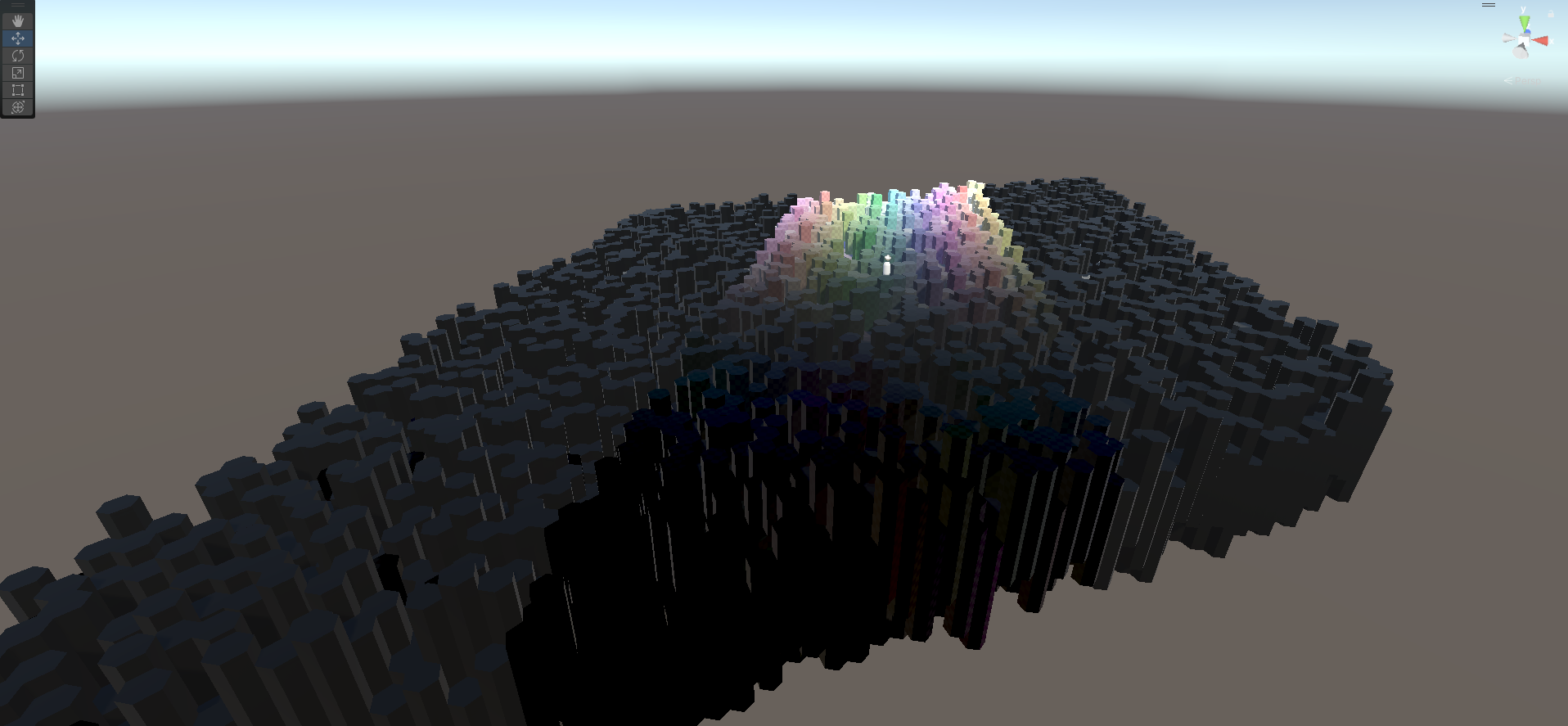
The first working version of the world generation algorithm.
It couldn't do anything complicated like biomes and decorations yet (besides, I hadn't made those yet), but it could fill the grid with hexagons and that's all I needed it to do to start.
But, if you take a moment to look at the result, you start to realise that this hexagon game is now generating in a large rhombus.
This, by itself, isn't really a problem. There's nothing wrong with a rhombus, honestly.
It's just that, when world generation is in the shape of a rhombus it starts to get a little difficult to control the dimensions of the generated world.
The North-South generation was fairly easy to control. That was one of my two generational axes, so it generated in a straight line.
West-East, on the other hand...
Since this axis was diagonal (North-East to South-West, in this image), from a top-down view each hex added almost as much 'height' as it did 'width'.
And it generated at that slanted angle, meaning there were more hexagons in the top-right and bottom-left than the other 2 corners, which meant that either there would be gaps in two corners of the average (rectangular) screen without hexes, or there would be a huge number of hexes beyond the edges of the screen.
The latter looked better, but took a lot more time and processing power to generate enough hexes.
Speaking of processing power, it was around this time that I noticed that some spots were being double, or even triple, filled.
Remember when I said the main downside to my 'diagonal axis' method was that it was a little more difficult to figure out the distance between hexes?
Turns out that, if I wasn't careful, the algorithm would sometimes end up picking the same spot multiple times to place a new hex.
The problems were starting to pile up. Obviously I was missing something important.
So I looked up an explanation/tutorial on the math behind hexagonal grids (and felt a bit silly that I hadn't thought of that in the first place, instead of trying to reinvent the wheel all by my lonesome)
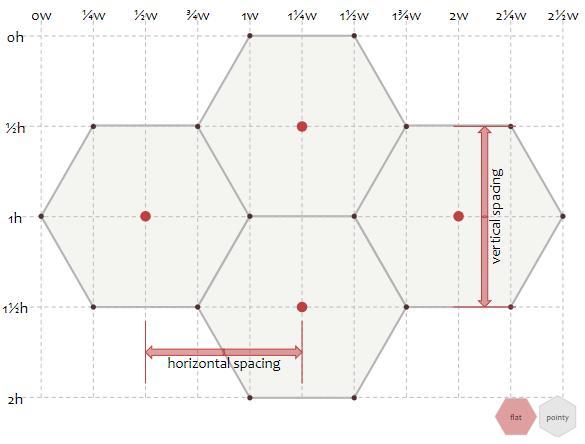
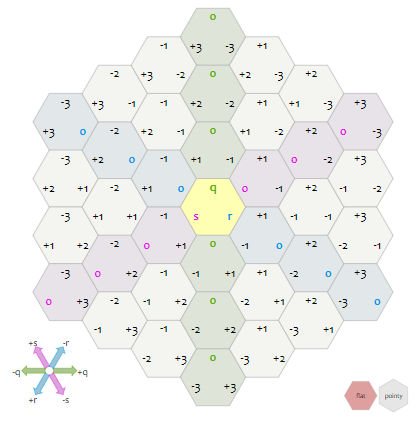
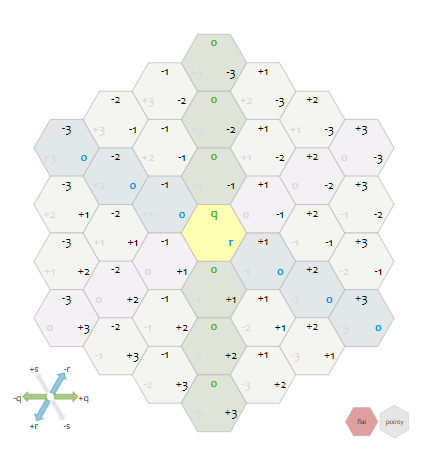
After looking through the explanations and the very helpful diagrams, I figured out that I had gotten pretty close and with a few corrections my code would still be useable.
So after fixing it up (and later making improvements using the newfound knowledge I had acquired) I was able to make much more suitably hexagonal grids.
Ranging from a large hexagon made of smaller hexagons:

To hexagonal 'lines' with variable thickness and length:


And that's the gist of basic world generation in this game.
Maybe I'll write up how biomes are handled, or how each hex gets its trees, rocks, and other little decorations chosen in a future devlog.
Until next time!
Get What, Once, was Here?
What, Once, was Here?
Explore and uncover the history of a lost civilisation while managing your supplies
| Status | Released |
| Author | DimlightGames |
| Genre | Adventure |
| Tags | 3D, Exploration, Indie, Isometric, Low-poly, Mystery, Roguelite, Singleplayer, Unity |
| Languages | English |
More posts
- Update 1.0.0 - full releaseApr 14, 2025
- Update 0.9.4Jan 09, 2025
- Decorating the WorldDec 06, 2024
- Biome Generation - Voronoi NoiseNov 22, 2024
- Update 0.9.3 - Events, Compass, and SkyboxNov 08, 2024
- Slow weekNov 01, 2024
- Dark Fantasy Studios - MusicOct 25, 2024
- Synty Studios - 3D assetsOct 18, 2024
- Future BiomesOct 11, 2024
Leave a comment
Log in with itch.io to leave a comment.